Setup code
library(simstudy)
library(cmdstanr)
library(posterior)
library(dplyr)
library(bayesplot)
library(ggplot2)
library(patchwork)
SEED <- 1234
set.seed(SEED)Distributional robustness in Bayesian inference
Many popular models are subject to strong parametric assumptions: the Gaussian noise of linear regression and the Gaussian innovations of auto-regressive processes to name but two. Their ubiquitous and casual application brings into sharp relief the precarious nature of many contemporary models. Distributional robustness remedies this potential danger by asserting no distributional assumptions on the uncertainty.
Generalised Bayesian inference (Bissiri, Holmes, and Walker 2016) offers an optimisation-centric learning paradigm in which one performs their belief update in terms of a loss function \(\ell\),
\[ q(\theta\mid x) \propto \exp\{-\ell(\theta, x)\} \pi(\theta). \]
And Knoblauch et al. (2019) show that a generalised Bayesian posterior \(q^\ast(\theta\mid x)\) follows from the solution to the infinite-dimensional optimisation problem
\[ q^\ast(\theta\mid x) = \arg\min_{q\in\mathscr{Q}(\Theta)} \left\{ \mathbb{E}_{\theta\sim q}\left [ n\cdot \mathbb{E}_{x\sim\mathbb{P}_n} \left [ \ell(x, \theta) \right ] \right ] + \mathbb{KL}(q\lVert \pi) \right \}, \tag{1}\]
where \(q\) indexes a distribution in the space of all probability measures on \(\Theta\), denoted \(\mathscr{Q}(\Theta)\), and \(\mathbb{KL}\) denotes the Kullback-Leibler (KL) divergence (Kullback and Leibler 1951). We take the data to be sampled from the empirical measure constructed from the data samples, \(\mathbb{P}_n = \frac{1}{n}\sum_{i=1}^n\delta_{x_i}\), where \(\delta_x\) is the Dirac measure at \(x\).
The first term of the generalised Bayesian objective is an expectation over a loss function with respect to the posterior. Scarf (1957) articulates his concerns with such average-case optimisation approaches, stating that an assumption is intrinsically made that the distribution of future data will be exactly that of the observed data.
This assumption is known to be violated in a great many instances. Distributionally robust optimisation (DRO) offers an innovation on this objective wherein one introduces an adversary capable of perturbing the data-generating distribution with a given budget (Scarf 1957; Kuhn et al. 2019; Namkoong and Duchi 2017). Their budget \(\epsilon\) is defined in terms of the distance between the nominal distribution and the perturbed distribution. We are primarily interested in integral probability metrics (IPMs) to quantify this distance. For a class of measurable and bounded functions \(\mathscr{F}\) mapping from the Polish space \(\Omega\) to \(\mathbb{R}\) with respect to the \(\sigma\)-algebra on \(\Omega\), the metric on \(\mathbb{P}, \mathbb{Q} \in \mathscr{Q}(\Omega)\),
\[ d_\mathscr{F}(\mathbb{P}, \mathbb{Q}) := \sup_{h\in\mathscr{F}}\left( \int_\Omega h \,\mathrm{d}\mathbb{P} + \int_\Omega h \,\mathrm{d}\mathbb{Q} \right) \]
is called the \(\mathscr{F}\)-integral probability metric between \(\mathbb{P}\) and \(\mathbb{Q}\) for the function \(h:\Omega\mapsto\mathbb{R}\). We further define the \(\mathscr{F}\)-ball centred on \(\mathbb{P}\) as \(B_{\epsilon, \mathscr{F}}(\mathbb{P}) := \{\mathbb{Q};\, d_\mathscr{F}(\mathbb{P}, \mathbb{Q}) \leq \epsilon \}\). In an average-case optimisation problem, one wishes to optimise the value of parameter \(\theta\) minimising an expected loss \(\ell\) and some observed data \(x\). We convert this into a DRO problem by taking the expectation in terms of the worst-case distribution within the \(\mathscr{F}\)-ball centred on \(\mathbb{P}_n\),
\[ \arg\min_{\theta\in\Theta} \sup_{\mathbb{Q}\in B_{\epsilon, \mathscr{F}}(\mathbb{P}_n)}\mathbb{E}_{x\sim\mathbb{Q}}\left [ \ell(\theta, x) \right ]. \]
While exact solutions to certain IPM DRO problems exist, they come at a high computational cost. Instead of deriving exact penalties, Husain (2020) shows that we can upper bound the IPM DRO objective in terms of the smallest multiplicative factor \(\Lambda_{\mathscr{F}}(\ell)\) required to stretch the convex hull of \(\mathscr{F}\) to contain our loss function \(\ell\). These bounds are usually easier to compute than the exact analytic penalties, and under specific choices of IPMs can encode some regularisation.
Returning then to the infinite-dimensional optimisation problem of Equation 1, denote \(q^\ast_{\epsilon, \mathscr{F}}(\theta\mid x)\) the distributionally robust Bayes posterior with uncertainty set admitting an \(\mathscr{F}\)-IPM with budget \(\epsilon\). Following Husain (Corollary 1, 2020), we can replace the supremum over the \(\mathscr{F}\)-ball with the infimum over the multiplicative factor to achieve the distributionally robust generalised Bayesian posterior
\[ q^\ast_{\epsilon, \mathscr{F}}(\theta\mid x) = \arg\min_{q\in\mathscr{Q}(\Theta)} \left\{ \mathbb{E}_{\theta\sim q}\left [ n\cdot \left ( \mathbb{E}_{x\sim\mathbb{P}_n} \left [ \ell(x, \theta) \right ] + \epsilon\cdot\inf_{b\in\mathbb{R}}\{ \Lambda_{\mathscr{F}}(\ell(x, \theta) - b) \} \right ) \right ] + \mathbb{KL}(q\lVert \pi) \right \} . \tag{2}\]
We budget our effort in this post to consider two primary IPMs: \(\mu\)-Fisher and \(\mu\)-Sobolev divergences.
A motivating example with Stan
As seems to the be becoming the themes in these posts, our first port of call is to Stan. If you are unfamiliar with this topic, please first have a look at my previous post.
Linear regression
We expose the problem naïvely by fitting a linear regression with standard Bayesian inference, that is setting \(\ell\) to be the negative log likelihood, and investigate two distributionally-robust innovations on it.
The \(\mu\)-Fisher divergence is formally defined as $$ _{}((x, ) = .
$$ For computational reasons we will take \(\mu\) in this expectation to be the empirical distribution (so the sample mean). Husain [Lemma 11, -Husain (2020)] shows that
$$
{b}{ {}((x, ) - b) } = ,
$$
and the IPM’s infimum is nothing more than the sample standard deviation. Well, implementing this is Stan is not so difficult, indeed we need only define this supplementary adversary and their budget.
data {
int<lower=0> N;
int<lower=0> p;
real<lower=0> budget; // adversary budget
matrix[N, p] x;
vector[N] y;
}
parameters {
real<lower=0> sigma;
vector[p] beta;
}
transformed parameters {
// compute the DRO term in the Bayesian update
vector[N] log_liks;
for (n in 1:N) {
log_liks[n] = normal_lpdf(y[n] | x[n] * beta, sigma);
}
real adversary = sd(log_liks);
}
model {
// priors
target += normal_lpdf(sigma | 0, 1);
for (j in 1:p) {
target += normal_lpdf(beta[j] | 0, 1);
}
// likelihood
target += normal_lpdf(y | x * beta, sigma);
// DRO adversary
target += -N * budget * adversary;
}Likewise, the \(\mu\)-Sobolev IPM is by definition
$$
_{}((x, ) = ,
$$
and thus once more by Lemma 11 from Husain (2020), its infimum can be written as
$$
{b}{ {}((x, ) - b) } = .
$$
Well once more in Stan, this is easy to implement.
functions {
real fprime(real y, real m, real s){
return(-(y - m) / square(s));
}
}
data {
int<lower=0> N;
int<lower=0> p;
real<lower=0> budget; // adversary budget
matrix[N, p] x;
vector[N] y;
}
parameters {
real<lower=0> sigma;
vector[p] beta;
}
transformed parameters {
// compute the DRO term in the Bayesian update
vector[N] h_x_nabla;
for (n in 1:N) {
h_x_nabla[n] = abs(fprime(y[n], x[n] * beta, sigma));
}
real adversary = sd(h_x_nabla);
}
model {
// priors
target += normal_lpdf(sigma | 0, 1);
for (j in 1:p) {
target += normal_lpdf(beta[j] | 0, 1);
}
// likelihood
target += normal_lpdf(y | x * beta, sigma);
// DRO adversary
target += -N * budget * adversary;
}OK, so it’s easy to add an adversary to a linear regression in Stan. Great. But how do we treat the adversary, and when do we expect it to help?
How much budget should your adversary get?
We will equip our adversary with a budget equal to \(\epsilon = n^{-2}\). This is to ensure that as \(n\to\infty,\,\epsilon\to 0\), and further that the term \(n\epsilon\to 0\) in the objective function of Equation 2.
This is quite a loose asymptotic argument for a bound on \(\epsilon\) (since we could equally have set \(\epsilon = n^{-3}\) to achieve the same guarantees). It may be that in individual circumstances, practitioners can use this budget term as a flavour of hyper-prior over data reliability.1
When is distributional robustness important?
Show code
# define experiment vars
N <- 100
Ntest <- N
p <- 10
mu_contam <- 10
sigma_clean <- 1
eps <- 0.2 # contamination ratio
# define the DGP
generate_clean_data <- function(n, p, mu_contam, sigma_clean, eps, ...) {
# Generate clean data using simstudy
def <- defRepeat(nVars = p, prefix = "x", formula = "0",
variance = "..sigma_clean", dist = "normal")
def <- defData(def, varname = "y", formula = lin_formula,
dist = "normal", variance = "..sigma_clean")
genData(n, def)
}
generate_contaminated_data <- function(n, p, mu_contam, sigma_clean, eps, ...) {
# First generate clean data
def <- defRepeat(nVars = p, prefix = "x", formula = "0",
variance = "..sigma_clean", dist = "normal")
def <- defData(def, varname = "yInlier", formula = lin_formula,
dist = "normal", variance = "..sigma_clean")
def <- defData(def, varname = "yOutlier", formula = "..mu_contam")
clean_data <- genData(n, def)
# Generate contaminated data using simstudy
clean_data |>
mutate(rsample = runif(n),
is_outlier = case_when(rsample < eps ~ TRUE,
rsample > eps ~ FALSE),
y = case_when(rsample < eps ~ yOutlier,
rsample > eps ~ yInlier)) |>
select(-rsample)
}
beta <- rep(.1, p)
lin_formula <- genFormula(beta, sprintf("x%s", 1:p))
# Generate the data using the provided generator function
dd_train <- generate_contaminated_data(N, p, mu_contam, sigma_clean, eps)
dd_test <- generate_clean_data(Ntest, p, mu_contam, sigma_clean, eps)
# produce Stan data
x <- as.matrix(dd_train)[, paste0("x", 1:p)]
x_test <- as.matrix(dd_test)[, paste0("x", 1:p)]
budget <- 1 / N^2
stan_data <- list(N = N,
Ntest = Ntest,
p = p,
x = x,
x_test = x_test,
y = dd_train$y,
y_test = dd_test$y,
budget = budget)
# compile and fit the vanilla Bayes model
exec_llk <- cmdstan_model(stan_file = file.path("../stan", "linreg_llk.stan"))
fit_llk <- exec_llk$sample(data = stan_data,
chains = 4,
parallel_chains = 4,
refresh = 0,
seed = SEED)
# extract predictions
yrep <- fit_llk$draws(variables = "yrep") |>
merge_chains() |>
as.data.frame() |>
as.matrix()
# plot posterior predictive
p_llk <- ppc_dens_overlay(dd_test$y, yrep[1:25, ]) +
theme_bw() +
theme(plot.background = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank()) +
labs(subtitle = "No adversary")
# compile and fit the mu Fisher Bayes model
exec_mu_fisher <- cmdstan_model(stan_file = file.path("../stan", "linreg_mu_fisher_dro.stan"))
fit_mu_fisher <- exec_mu_fisher$sample(data = stan_data,
chains = 4,
parallel_chains = 4,
refresh = 0,
seed = SEED)
# extract predictions
yrep_fisher <- fit_mu_fisher$draws(variables = "yrep") |>
merge_chains() |>
as.data.frame() |>
as.matrix()
# plot posterior predictive
p_fisher <- ppc_dens_overlay(dd_test$y, yrep_fisher[1:25, ]) +
theme_bw() +
theme(plot.background = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank()) +
labs(subtitle = "mu-Fisher")
# compile and fit the mu Sobolev Bayes model
exec_mu_sobolev <- cmdstan_model(stan_file = file.path("../stan", "linreg_mu_sobolev_dro.stan"))
fit_mu_sobolev <- exec_mu_sobolev$sample(data = stan_data,
chains = 4,
parallel_chains = 4,
refresh = 0,
seed = SEED)
# extract predictions
yrep_sobolev <- fit_mu_sobolev$draws(variables = "yrep") |>
merge_chains() |>
as.data.frame() |>
as.matrix()
# plot posterior predictive
p_sobolev <- ppc_dens_overlay(dd_test$y, yrep_sobolev[1:25, ]) +
theme_bw() +
theme(plot.background = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank()) +
labs(subtitle = "mu-Sobolev")
# combine the plots and make pretty
p_combined <- (p_llk / p_fisher / p_sobolev)
p_ranges_x <- c(ggplot_build(p_combined[[1]])$layout$panel_scales_x[[1]]$range$range,
ggplot_build(p_combined[[2]])$layout$panel_scales_x[[1]]$range$range)
p_ranges_y <- c(ggplot_build(p_combined[[1]])$layout$panel_scales_y[[1]]$range$range,
ggplot_build(p_combined[[2]])$layout$panel_scales_y[[1]]$range$range)Distributional robustness, intuitively, should be most important when the training and test data distributions differ greatly.
As such, we begin by generating some data from a toy contamination linear regression example, we simulate predictors \(x_{j} \sim\mathrm{normal}(0,1)\) for \(j = 1,\dotsc,p\), and then generate the target \(y\) according to
$$
y(1-),(^x, 1^2) +,_{10},
$$ where \(\delta_{10}\) is the Dirac delta function at \(10\), and \(\beta = (0.1,\dotsc,0.1)^\top\).
We generate \(n = 100\) such contaminated training observations for \(p = 10\) predictors with a contamination rate \(\lambda = 0.2\), fit our linear regression to these contaminated training data, and then evaluate its predictions on clean test data (meaning \(\lambda = 0\)). We do this for one linear regression without any adversary, and two with a \(\mu\)-Fisher and \(\mu\)-Sobolev adversary respectively.
Show code
# produce the final plot
p_combined &
xlim(min(p_ranges_x), max(p_ranges_x)) &
ylim(min(p_ranges_y), max(p_ranges_y))
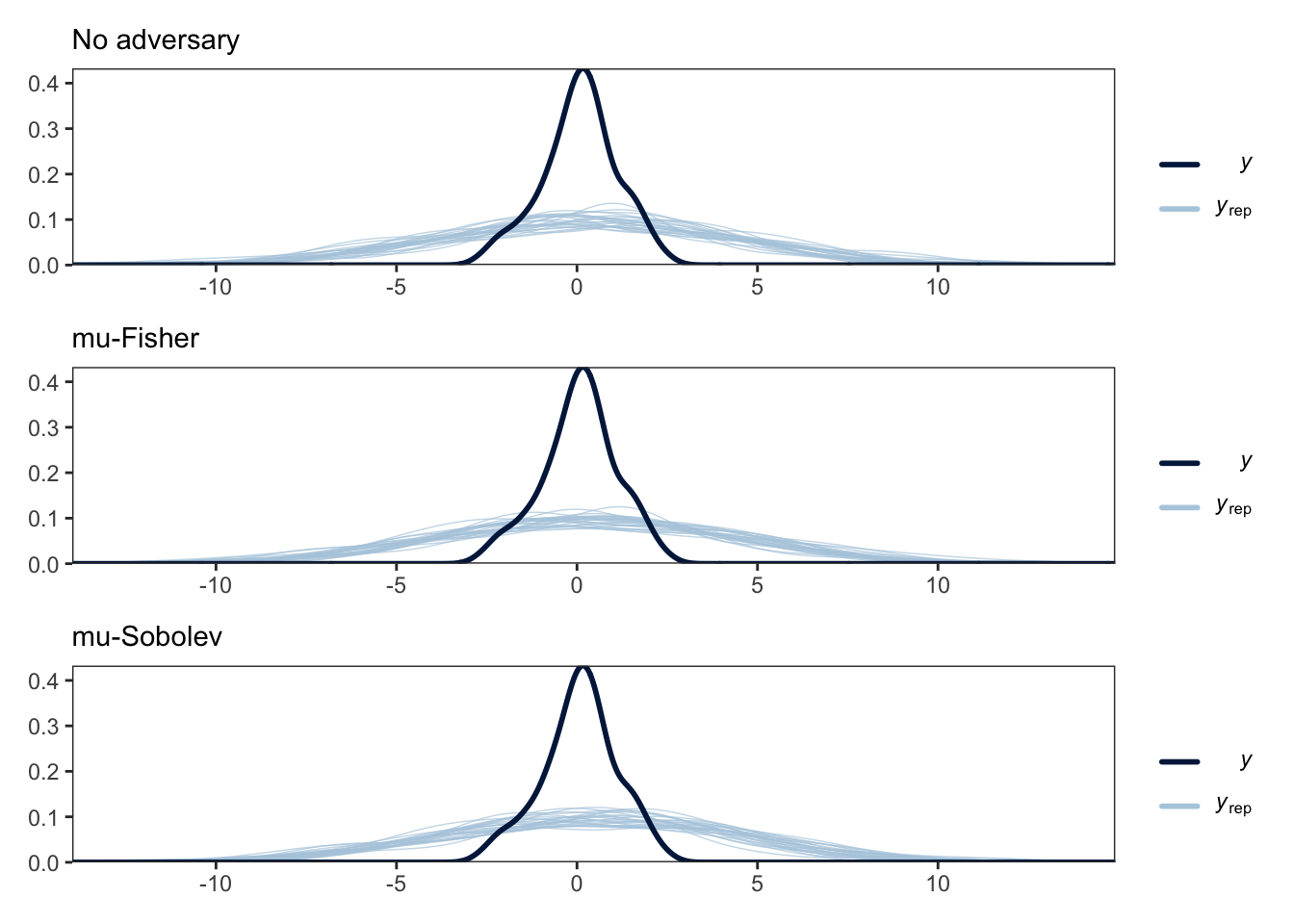
This plots shows the empirical distribution of the test data (in dark blue) compared to the distributions of simulated data, \(y_\mathrm{rep}\) (in light blue), from the posterior predictive distribution of the three models.
We would hope that the adversary would be able to filter out the noise in the training data and thus produce more representative predictive distributions. In this example, at least, we don’t see much. It may be that since the adversary’s budget shrinks so quickly with \(n\), it performs negligible correction.
References
Bissiri, Pier Giovanni, Chris Holmes, and Stephen Walker. 2016. “A General Framework for Updating Belief Distributions.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 78 (5): 1103–30. https://doi.org/10.1111/rssb.12158.
Husain, Hisham. 2020. “Distributional Robustness with IPMs and Links to Regularization and GANs.” In Proceedings of the 34th International Conference on Neural Information Processing Systems. NIPS’20. Red Hook, NY, USA: Curran Associates Inc.
Knoblauch, Jeremias, Jack Jewson, and Theodoros Damoulas. 2019. “Generalized Variational Inference: Three Arguments for Deriving New Posteriors.” arXiv. https://doi.org/10.48550/arXiv.1904.02063.
Kuhn, Daniel, Peyman Mohajerin Esfahani, Viet Anh Nguyen, and Soroosh Shafieezadeh-Abadeh. 2019. “Wasserstein Distributionally Robust Optimization: Theory and Applications in Machine Learning.” In Operations Research &Amp; Management Science in the Age of Analytics, 130–66. INFORMS. https://doi.org/10.1287/educ.2019.0198.
Kullback, S., and R. A. Leibler. 1951. “On Information and Sufficiency.” The Annals of Mathematical Statistics 22 (1): 79–86. https://doi.org/10.1214/aoms/1177729694.
Namkoong, Hongseok, and John C Duchi. 2017. “Variance-Based Regularization with Convex Objectives.” In Advances in Neural Information Processing Systems, edited by I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett. Vol. 30. Curran Associates, Inc. https://proceedings.neurips.cc/paper/2017/file/5a142a55461d5fef016acfb927fee0bd-Paper.pdf.
Scarf, Herbert E. 1957. A Min-Max Solution of an Inventory Problem. Santa Monica, CA: RAND Corporation.
Footnotes
Please feel free to reach out if you have any ideas on how this could be made more concrete.↩︎
Citation
BibTeX citation:
@online{mclatchie2023,
author = {Yann McLatchie},
title = {Distributionally Robust Posteriors with Integral Probability
Metrics},
date = {2023-10-05},
url = {https://yannmclatchie.github.io/blog/posts/dro-bayes},
langid = {en}
}
For attribution, please cite this work as:
Yann McLatchie. 2023. “Distributionally Robust Posteriors with
Integral Probability Metrics.” October 5, 2023. https://yannmclatchie.github.io/blog/posts/dro-bayes.